Magnetic Fusion Energy
核融合反応
太陽などの恒星の内部ではpp連鎖とよばれる一連の反応により、水素Hから重水素D、ヘリウム3Heを経てヘリウム4Heが作られ、膨大なエネルギーが放出されます。この反応のうち、HからDが作られる反応が非常にゆっくりと進行し、恒星の寿命を決めています。 効率よくエネルギーを取り出すには、反応速度係数〈σv〉の大きな反応を選ぶ必要があります。代表的な核融合反応に次のようなものがあります。
| D + T | → | 4He (3.52 MeV) + n (14.06 MeV) | |
| D + D | → | T (1.01 MeV) + H (3.03 MeV) | |
| 3He (0.82 MeV) + n (2.45 MeV) | |||
| D + 3He | → | 4He (3.67 MeV) + H (14.67 MeV) |
三重水素Tは原子核反応によって生成される物質です。2 gのDと3 gのTから1.7×1012 Jのエネルギーが生み出され、100万kWの電力を28分間にわたって維持することができます。
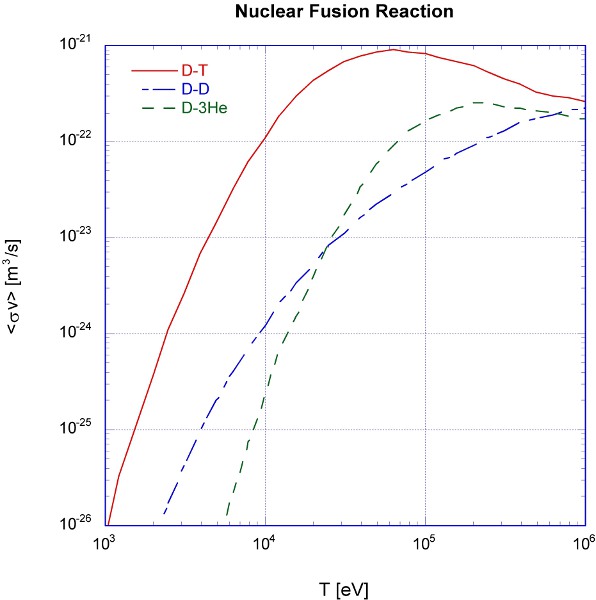
炉心プラズマの温度を2億度(20 keV)とすると、反応速度係数は〈σv〉 = 4.3×10-22 [m3/s] となります。
定常核融合炉
DT核融合反応の発生はDの密度をnD、Tの密度をnTとすると、単位時間当たりnDnT〈σv〉です。これに反応で発生するエネルギーとプラズマの体積をかけたものが核融合出力となります。
密度をnD = nT = 1020 [m-3] とすると、100万kWの出力を得るために必要なプラズマの体積は80 m3になります。このプラズマの圧力は13 気圧、熱エネルギーは100 MJにもなります。これは時速80 kmで走る400トンの列車の運動エネルギーに匹敵します。
このプラズマのエネルギーを維持するためには、絶えずエネルギーを加えてプラズマを加熱する必要があります。熱エネルギーWTと加熱電力Pinとの比を閉じ込め時間τといい、核融合装置の効率の良さを表します。閉じ込め時間はプラズマが点灯している時間ではありません。
τ = WT/Pin
核融合出力Poutと加熱電力Pinとの比をQ値といいます。
Q = Pout/Pin
Q = 10 とするとτ = 1 秒が要求されることになります。現在このような性能を持つ装置はトカマクしかありません。
技術的課題
温度2億度、DとTを合わせた密度2×1020/m3、閉じ込め時間1秒をすべて同時に満足することは、それほど困難ではないと考えられます。また、トカマクではプラズマ中に電流を流し続ける必要がありますが、この問題はほぼ解決されています。
核融合出力の80 %、すなわち80万kWは中性子nとして放出されます。このエネルギーはリチウムブランケットを用いて回収されます。残りの20 %は4He(α粒子)として放出されます。この粒子が炉心に残ってプラズマを加熱することはあまり期待できず、加熱電力とあわせた30万kWがダイバータとよばれる粒子回収装置に行くことになります。ダイバータは不純物除去のための補助的な手段ではなく、核融合出力を回収するという重要な手段を担うことになります。強烈な熱負荷に耐えるダイバータの開発が最大の課題となっています。
プラズマ中に発生する巨視的な不安定性によってプラズマ全体が崩壊する現象をディスラプションといいます。ディスラプションが起こると、100 MJもの熱エネルギーが一瞬にして放出されることになります。ディスラプションは起こらないようにすることが最善の策ですが、万が一起こった場合にも第一壁に損傷を与えないように制御し、そのエネルギーを分散吸収するしくみが重要です。